Introduction to Linked Lists
Overview of Linked Lists
- Definition: A linked list is a linear data structure where each element (called a node) contains a data part and a reference (or link) to the next node in the sequence.
- Characteristics: Linked lists are dynamic in size, easily allowing insertion and deletion of elements without reallocation or reorganization of the entire structure.
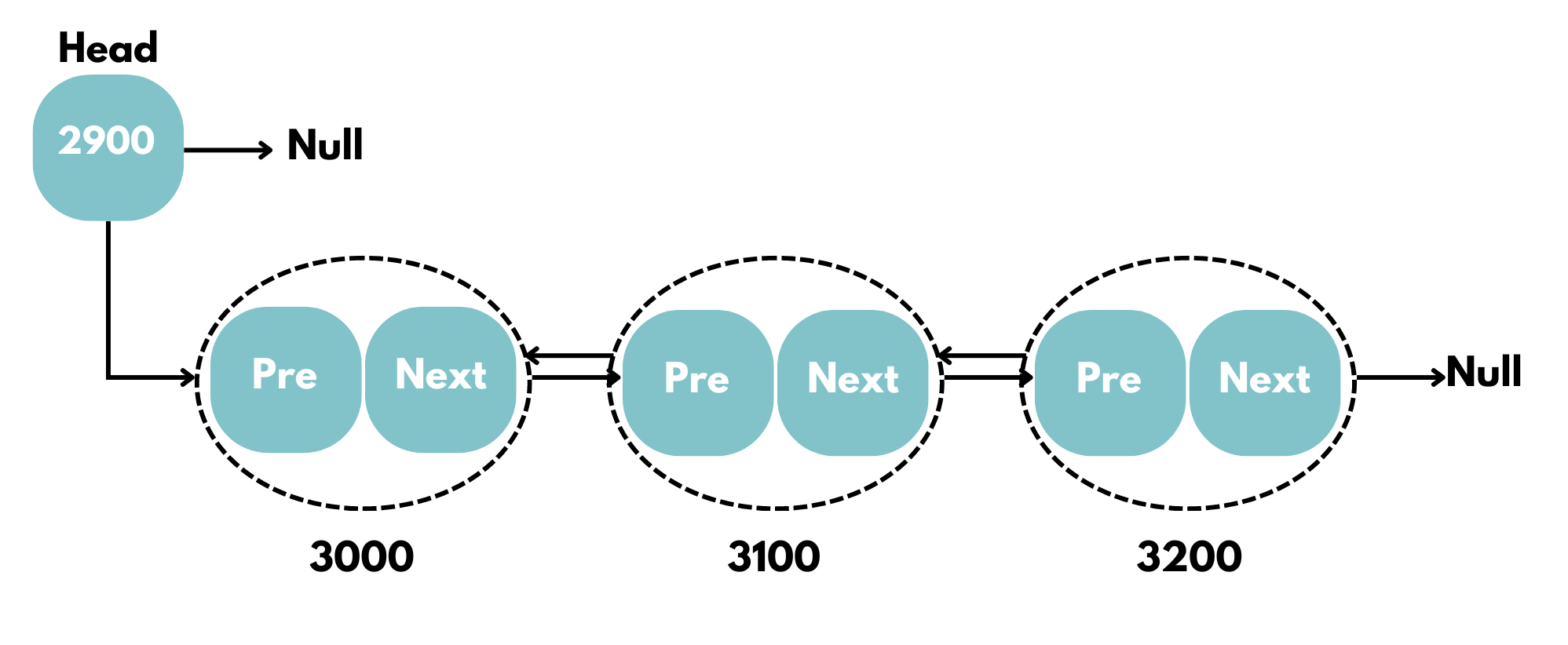
Definition and Characteristics
- Nodes: Basic building blocks of linked lists, consisting of a data field and a reference to the next node.
- Head: The first node in the linked list. It is used as a starting point to traverse the list.
- Tail: The last node in the linked list, where the following reference is null (in singly linked lists) or points back to the head (in circular linked lists).
- Null Reference: Used to signify the end of the list (in singly linked lists) or absence of nodes.
- Dynamic Size: Linked lists do not have a fixed size and can grow or shrink as elements are added or removed.
- Memory Allocation: Nodes are dynamically allocated in heap memory.
Comparison with Arrays
| Aspect | Arrays | Linked Lists |
|---|---|---|
| Memory Allocation and Management | ||
| Static vs Dynamic | Fixed size, requiring contiguous memory allocation. Size is defined at the time of declaration. | Dynamic size, with nodes allocated on the heap. No need for contiguous memory. |
| Access Time | ||
| Indexing | O(1) time complexity for accessing any element using the index. | O(n) time complexity for accessing an element, as it requires traversal from the head to the desired node. |
| Insertion and Deletion | ||
| Operations | Insertion and deletion operations are O(n) on average, as they may require shifting elements. | Insertion and deletion are O(1) if the position is known (e.g., at the head or tail), but O(n) for arbitrary positions due to traversal time. |
| Memory Overhead | ||
| Extra Storage | No extra storage required beyond the array itself. | Additional memory required for storing pointers/references in each node. |
| Flexibility | ||
| Size Adjustment | Size is fixed; changing size requires creating a new array and copying elements. | Size can be adjusted easily by adding or removing nodes. |
| Traversal and Operations | ||
| Traversal | Can be traversed using simple loops with index manipulation. | Requires pointer manipulation to traverse from one node to the next. |
| Memory Utilization | ||
| Fragmentation | Contiguous memory allocation can lead to memory fragmentation if arrays are frequently resized. | Non-contiguous memory allocation can better utilize fragmented memory but may lead to more complex memory management. |
Importance of Understanding Complexity
Understanding time and space complexity is crucial for several reasons, particularly in the context of software development. Here’s a detailed exploration of its significance:
Time and Space Complexity in Context
1. Efficiency of Algorithms:
- Time complexity refers to the computational time required by an algorithm to complete its task as a function of the input size. Understanding this helps developers choose the most efficient algorithms for their specific problems, ensuring that applications run quickly, especially as data sizes grow.
- Space complexity deals with the amount of memory an algorithm uses. It includes both the space required by the input data and the space required for auxiliary data structures. Knowing space complexity is essential in environments with limited memory resources.
2. Scalability:
- As applications scale and data volumes increase, algorithms that are efficient in terms of time and space complexity become increasingly important. A linear-time algorithm might be feasible for small datasets but can become impractical as the dataset grows exponentially. Understanding complexity helps predict how an application will perform under load.
3. Resource Management:
- Efficient algorithms can significantly reduce resource consumption. For example, in environments where CPU cycles or memory are at a premium (like mobile devices or embedded systems), choosing algorithms with favorable complexity metrics can enhance performance and battery life.
Practical Implications for Software Development
1. Performance Optimization:
- Developers must frequently optimize existing code. By analyzing time and space complexity, they can identify bottlenecks and refactor code to use more efficient algorithms or data structures, leading to better performance.
2. Algorithm Selection:
- Different problems require different algorithms. Understanding complexity helps developers evaluate options and select the most appropriate one based on expected input sizes and constraints. For instance, using a quicksort for large datasets instead of a bubble sort can lead to significant performance improvements.
3. Code Review and Maintenance:
- During code reviews, understanding complexity allows developers to assess whether the chosen approaches are suitable. This awareness is essential for long-term code maintenance and ensuring that future enhancements do not degrade performance.
4. User Experience:
- In user-facing applications, performance directly impacts user experience. Slow operations can frustrate users and lead to decreased satisfaction and engagement. By prioritizing algorithms with good time complexity, developers can ensure smoother and faster interactions.
5. System Design:
- In designing systems, especially distributed systems, understanding complexity aids in architectural decisions. It helps determine how data is stored, processed, and retrieved, balancing trade-offs between time and space across different components of the system.
6. Real-World Constraints:
- Real-world applications often face constraints such as memory limits, processing power, and response time requirements. Understanding complexity allows developers to work within these constraints effectively, ensuring that the application can operate under expected conditions without failing.
7. Predicting Behavior:
- Analyzing the time and space complexity of algorithms provides insights into their behavior as input sizes grow. This predictive capability is essential for anticipating how changes in data volume will affect application performance.
In summary, understanding time and space complexity is fundamental for software developers, influencing algorithm selection, performance optimization, and system design. It ensures that applications are efficient, scalable, and capable of delivering a positive user experience, ultimately leading to more robust and maintainable software solutions.
Types of Linked List
Here’s a detailed breakdown of the types of linked lists, including their structures and operations, in tabular form.
| Type of Linked List | Description |
|---|---|
| Singly Linked List | |
| Structure | Consists of nodes with two parts: a data field and a reference to the next node. |
| Basic Operations | – Insertion: Add a node at the beginning, end, or after a specific node. – Deletion: Remove a node from the beginning, end, or specific position. – Traversal: Visit each node starting from the head. – Search: Find a node with a specific value. |
| Doubly Linked List | |
| Structure | Consists of nodes with three parts: a data field, a reference to the next node, and a reference to the previous node. |
| Differences from Singly Linked List | – Bidirectional Traversal: Can traverse in both directions (forward and backward). – Extra Memory: Requires more memory due to the additional pointer. – Insertion/Deletion: Easier to remove a node given only the node reference, as it allows access to the previous node. |
| Circular Linked List | |
| Unique Properties | The last node points back to the first node, creating a circular structure. |
| Use Cases | – Useful for applications requiring a circular iteration, such as round-robin scheduling. – Efficient in scenarios where the list needs to be continuously traversed without reaching an end. |
This table provides a concise overview of the types of linked lists, highlighting their structures, operations, differences, and unique properties.
Insertion Operations in Linked Lists
Insertion at the Beginning
Inserting a node at the beginning of a singly linked list involves the following steps:
- Create a New Node: Allocate memory for a new node and set its data field to the value you want to insert.
- Update the New Node’s Pointer: Set the
nextpointer of the new node to point to the current head of the linked list. This effectively links the new node to the existing list.
- Update the Head: Change the head of the linked list to be the new node. Now, the new node is the first element of the list.
Here’s a simple representation in pseudocode:
function insertAtBeginning(head, value):
newNode = createNode(value) // Step 1
newNode.next = head // Step 2
head = newNode // Step 3
return headTime Complexity Analysis
- Time Complexity: O(1)
- The insertion at the beginning of the list takes constant time because it involves a fixed number of operations regardless of the size of the list. No traversal is needed; you simply update pointers.
Space Complexity Analysis
- Space Complexity: O(1)
- The space complexity is also constant, as the only additional space used is for the new node that is being created. The size of the list does not affect the amount of memory required for this operation, apart from the node itself.
Detailed Code Examples
Insertion at the Beginning
C
//Insertion at the Beginning
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
void insertAtBeginning(struct Node** head, int newData) {
struct Node* newNode = (struct Node*) malloc(sizeof(struct Node));
newNode->data = newData;
newNode->next = *head;
*head = newNode;
}
void printList(struct Node* node) {
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
int main() {
struct Node* head = NULL;
insertAtBeginning(&head, 10);
insertAtBeginning(&head, 20);
insertAtBeginning(&head, 30);
printList(head);
return 0;
}C++
//Insertion at the Beginning
#include <iostream>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data) : data(data), next(nullptr) {}
};
void insertAtBeginning(Node*& head, int newData) {
Node* newNode = new Node(newData);
newNode->next = head;
head = newNode;
}
void printList(Node* node) {
while (node != nullptr) {
cout << node->data << " ";
node = node->next;
}
}
int main() {
Node* head = nullptr;
insertAtBeginning(head, 10);
insertAtBeginning(head, 20);
insertAtBeginning(head, 30);
printList(head);
return 0;
}JavaScript
//Insertion at the Beginning
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertAtBeginning(newData) {
const newNode = new Node(newData);
newNode.next = this.head;
this.head = newNode;
}
printList() {
let current = this.head;
while (current) {
console.log(current.data);
current = current.next;
}
}
}
const list = new LinkedList();
list.insertAtBeginning(10);
list.insertAtBeginning(20);
list.insertAtBeginning(30);
list.printList();Insertion at the End
C
//Insertion at the End
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
void insertAtEnd(struct Node** head, int newData) {
struct Node* newNode = (struct Node*) malloc(sizeof(struct Node));
struct Node* last = *head;
newNode->data = newData;
newNode->next = NULL;
if (*head == NULL) {
*head = newNode;
return;
}
while (last->next != NULL) {
last = last->next;
}
last->next = newNode;
}
void printList(struct Node* node) {
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
int main() {
struct Node* head = NULL;
insertAtEnd(&head, 10);
insertAtEnd(&head, 20);
insertAtEnd(&head, 30);
printList(head);
return 0;
}C++
//Insertion at the End
#include <iostream>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data) : data(data), next(nullptr) {}
};
void insertAtEnd(Node*& head, int newData) {
Node* newNode = new Node(newData);
if (head == nullptr) {
head = newNode;
return;
}
Node* last = head;
while (last->next != nullptr) {
last = last->next;
}
last->next = newNode;
}
void printList(Node* node) {
while (node != nullptr) {
cout << node->data << " ";
node = node->next;
}
}
int main() {
Node* head = nullptr;
insertAtEnd(head, 10);
insertAtEnd(head, 20);
insertAtEnd(head, 30);
printList(head);
return 0;
}JavaScript
//Insertion at the End
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertAtEnd(newData) {
const newNode = new Node(newData);
if (!this.head) {
this.head = newNode;
return;
}
let last = this.head;
while (last.next) {
last = last.next;
}
last.next = newNode;
}
printList() {
let current = this.head;
while (current) {
console.log(current.data);
current = current.next;
}
}
}
const list = new LinkedList();
list.insertAtEnd(10);
list.insertAtEnd(20);
list.insertAtEnd(30);
list.printList();Insertion in the Middle
C
//Insertion in the Middle
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
void insertAfter(struct Node* prevNode, int newData) {
if (prevNode == NULL) {
printf("The given previous node cannot be NULL");
return;
}
struct Node* newNode = (struct Node*) malloc(sizeof(struct Node));
newNode->data = newData;
newNode->next = prevNode->next;
prevNode->next = newNode;
}
void printList(struct Node* node) {
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
int main() {
struct Node* head = (struct Node*) malloc(sizeof(struct Node));
struct Node* second = (struct Node*) malloc(sizeof(struct Node));
struct Node* third = (struct Node*) malloc(sizeof(struct Node));
head->data = 10;
head->next = second;
second->data = 20;
second->next = third;
third->data = 30;
third->next = NULL;
insertAfter(second, 25);
printList(head);
return 0;
}C++
//Insertion in the Middle
#include <iostream>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data) : data(data), next(nullptr) {}
};
void insertAfter(Node* prevNode, int newData) {
if (prevNode == nullptr) {
cout << "The given previous node cannot be NULL" << endl;
return;
}
Node* newNode = new Node(newData);
newNode->next = prevNode->next;
prevNode->next = newNode;
}
void printList(Node* node) {
while (node != nullptr) {
cout << node->data << " ";
node = node->next;
}
}
int main() {
Node* head = new Node(10);
Node* second = new Node(20);
Node* third = new Node(30);
head->next = second;
second->next = third;
insertAfter(second, 25);
printList(head);
return 0;
}JavaScript
//Insertion in the Middle
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertAfter(prevNode, newData) {
if (!prevNode) {
console.log("The given previous node cannot be NULL");
return;
}
const newNode = new Node(newData);
newNode.next = prevNode.next;
prevNode.next = newNode;
}
printList() {
let current = this.head;
while (current) {
console.log(current.data);
current = current.next;
}
}
}
const list = new LinkedList();
list.head = new Node(10);
const second = new Node(20);
const third = new Node(30);
list.head.next = second;
second.next =
third;
list.insertAfter(second, 25);
list.printList();Time Complexity Analysis of Insertion at the Beginning
When analyzing the time complexity of inserting a new node at the beginning of linked lists, both singly and doubly linked lists exhibit O(1) time complexity. Here’s a detailed breakdown for each type:
Singly Linked List
Operation Steps:
- Create a New Node: Allocate memory for a new node and set its data.
- Point to the Current Head: Set the new node’s
nextpointer to the current head of the linked list.
- Update Head: Change the head pointer to point to the new node.
Time Complexity Breakdown:
- Memory Allocation: Allocating memory for the new node is a constant time operation, O(1).
- Pointer Assignment: Setting the
nextpointer of the new node to the current head is also O(1).
- Head Update: Updating the head pointer to the new node is O(1).
Since all the steps involved in inserting at the beginning require a fixed amount of time irrespective of the size of the linked list, the overall time complexity for inserting at the beginning of a singly linked list is:
Time Complexity: O(1)
Doubly Linked List
Operation Steps:
- Create a New Node: Similar to the singly linked list, allocate memory for a new node and set its data.
- Point to the Current Head: Set the new node’s
nextpointer to the current head.
- Update Head’s Previous Pointer: If the list is not empty, update the current head’s
prevpointer to point to the new node.
- Update Head: Change the head pointer to the new node.
Time Complexity Breakdown:
- Memory Allocation: Allocating memory for the new node takes O(1).
- Pointer Assignments:
- Setting the
nextpointer of the new node to the current head is O(1). - Updating the
prevpointer of the current head (if it exists) to point to the new node is also O(1).
- Setting the
- Head Update: Updating the head pointer to the new node is O(1).
Again, since each of these steps executes in constant time regardless of the size of the linked list, the overall time complexity for inserting at the beginning of a doubly linked list is:
Time Complexity: O(1)
Summary
In conclusion, both singly and doubly linked lists have the same time complexity for insertion at the beginning, which is O(1). This efficiency stems from the fact that the operation involves a fixed number of pointer assignments and memory allocation, making it ideal for scenarios where frequent insertions are required.
Space Complexity Analysis of Insertion Operations in Linked Lists
Singly Linked List
Insertion at the Beginning
- Space Complexity: O(1)
- Explanation: When inserting at the beginning, we create a new node and update the pointers. The space needed is constant and does not depend on the size of the list.
Insertion at the End
- Space Complexity: O(1)
- Explanation: Inserting at the end involves creating a new node and potentially updating the pointer of the last node to the new node. The space required is still constant.
Insertion in the Middle
- Space Complexity: O(1)
- Explanation: For insertion in the middle, we need to create a new node and adjust the pointers of the adjacent nodes. This operation also requires a constant amount of additional space.
Doubly Linked List
Insertion at the Beginning
- Space Complexity: O(1)
- Explanation: Similar to the singly linked list, inserting at the beginning in a doubly linked list requires creating a new node and updating the
nextandprevpointers. The space needed is constant.
Insertion at the End
- Space Complexity: O(1)
- Explanation: Inserting at the end involves creating a new node and updating the
nextpointer of the last node and theprevpointer of the new node. This operation requires a constant amount of additional space.
Insertion in the Middle
- Space Complexity: O(1)
- Explanation: Insertion in the middle involves creating a new node and adjusting the
nextandprevpointers of the adjacent nodes. This operation also requires a constant amount of additional space.
Summary
| Operation | Singly Linked List: Space Complexity | Doubly Linked List: Space Complexity |
|---|---|---|
| Operations | O(1) additional space | O(1) additional space |
| Insertion at End | O(1) additional space | O(1) additional space |
| Insertion in Middle | O(1) additional space | O(1) additional space |
The space complexity for insertion operations at the beginning, end, and middle of both singly and doubly linked lists is O(1). This is because each operation requires creating a single new node and updating a fixed number of pointers, regardless of the size of the list.
Practical Implications and Conclusion
Summary of Complexity
Insertion Complexities for Singly and Doubly Linked Lists:
Singly Linked List:
Insertion at Beginning: O(1) time, O(1) space
- Insertion at End: O(n) time, O(1) space
- Insertion in Middle: O(n) time, O(1) space
Doubly Linked List:
- Insertion at Beginning: O(1) time, O(1) space
- Insertion at End: O(1) time, O(1) space (if tail pointer is maintained)
- Insertion in Middle: O(n) time, O(1) space
Practical Considerations
When to Use Which Insertion Method:
Insertion at the Beginning:
- Use Cases: When elements need to be frequently added to the start, such as in stacks (LIFO structure) or when building the list in reverse order.
- Performance Implications: This method is efficient (O(1) time) and does not depend on the size of the list, making it ideal for applications with frequent insertions at the beginning.
Insertion at the End:
- Use Cases: When elements are typically added to the end, such as in queues (FIFO structure) or when appending elements to a list in order.
- Performance Implications: For singly linked lists, this operation is O(n) as it requires traversal to the end. For doubly linked lists with a maintained tail pointer, it is O(1), making it efficient for large datasets.
Insertion in the Middle:
- Use Cases: When elements need to be inserted at specific positions within the list, such as sorted lists or priority queues.
- Performance Implications: This method requires O(n) time for traversal, which can impact performance for large lists. However, it is useful when precise control over the insertion point is needed.
Performance Implications in Real-World Applications:
- Singly Linked Lists: Best suited for scenarios where insertions and deletions primarily occur at the beginning of the list. Applications include stack implementations, undo functionality in software, and reverse order data processing.
- Doubly Linked Lists: More versatile due to bidirectional traversal. Ideal for scenarios where frequent insertions/deletions occur at both ends or specific positions. Common use cases include complex data structures like deques, navigation systems (e.g., browser history), and implementing LRU (Least Recently Used) caches.
Conclusion
Key Takeaways:
Efficiency: Insertion operations at the beginning of both singly and doubly linked lists are highly efficient (O(1) time complexity), making them suitable for use cases requiring frequent head insertions.
- Insertion at End: More efficient in doubly linked lists with a tail pointer (O(1) time complexity) compared to singly linked lists (O(n) time complexity).
- Insertion in Middle: Generally less efficient due to O(n) traversal time but necessary for specific use cases requiring positional inserts.
Final Thoughts on Linked List Insertion Operations:
- Understanding the complexity of linked list operations is critical for making informed decisions in software development. By leveraging the appropriate insertion method based on specific requirements, developers can optimize performance and resource utilization.
- Singly linked lists offer simplicity and efficiency for head insertions, while doubly linked lists provide greater flexibility for a broader range of operations. Both structures are fundamental in computer science, underpinning more complex data structures and algorithms essential for effective software design.
Discover more from lounge coder
Subscribe to get the latest posts sent to your email.

